古曆程序隨記

問題

無中氣置閏

極端情況是，(MidTermAvgRaw[LeapNumMidTerm] >= FirstOrderRaw[LeapNumMidTerm + 1]) && (MidTermAvgRaw[LeapNumMidTerm] < FirstOrderRaw[LeapNumMidTerm + 1] + 2 最後的 2 改成 1.437，那就最多提前 1 次，改成 1.874，最多提前 2 次，改成 2，最多提前 3 次。但是不可能超出 2 了。所以提前 1 次到提前 3 次出現的概率是依次減小。

授時曆

• 没有寫有㒳个條件下的 FirstXianAnoma=什么，导致了 NaN。出現以下問題：1007，1011，1012，1023，1037，1038，1049，1052，1053，1059，1063，1075，1079，1085，1089，1094，1095 的定朔沒有最後一個月的干支，閏餘 nan，分 n
• 問題出在加減差，第一二月的太大了，導致定閏餘不對，導致連閏。問題出在遲疾差、FirstFaSlowV 太大。問題出在 FirstAnoma 沒有化成正數。1012-1013-1014-1015，1031-1032，1040-1041，1058-1059，1075-1076，1080-1081，1093-1094，1328-1329 經朔首尾是一樣的。1004 年最後一月只有 22 天。1011 年最後一月 32 天。1031、1032 連閏
• leapsuraccurate 沒有化成正數。曆元前無閏月。問題的根源就是很多參數沒化成正數。解決方法就是「模加模」。
• 曆元前錯開了一月，子月顯示了丑月的干支。剛開始通過曆元前的年份 -1 朔策。11-14 改成並行兩套系統，一套是經朔系統，把積日化成正數；一套是定朔系統，保留原來的負數。
• 曆元前中氣如果減去兩個朔策，冬至不對。那就減去一個中氣、一個朔策。但是後來又發現這樣還是不對，與把統積化成正數的正確方法比起來，這種方法在大約五分之二的年份，會有一個中氣相差一日。最後表都製好了，只能一年一年把授時曆的正確中氣粘貼過去。
• 最後的最後，發現原來不用那麼複雜，通積不用並行兩套，只要把閏餘化成正數就足夠了。

古曆

• 祖傳入蔀名稱問題從十天前剛開始編程就出現了，本以爲解決了，又出現，又解決，又出現，現在徹底解決。
• 又遇到入蔀年到底算上還是算外的問題。最後終於梳理清楚。崩潰。之前寫了那麼複雜的邏輯：

三統曆入統年的計算爲算外，需要在結果上 +1。四分曆若在計算中得出的結果是 0，實際情況是入紀年爲 76，這時需要人工加以規定。三統曆由於算外，就不存在這一問題，結果爲 0 時入統年爲 1。

1 2 3 4 5 6 7

var BuYear = OriginYear % YuanRange % JiRange % BuRange + ifTong if (BuYear == 0) { BuYear = 76 }

接下來計算蔀（統）序。四分曆在計算蔀序時需要減去一個很小的小數，目的是當入紀年除以蔀法 76 得整數，卽入蔀年爲 76 時，蔀序依然是上一蔀，而不是進位到下一蔀。

1	var BuOrder = Math.floor(OriginYear % YuanRange % JiRange / BuRange - 0.00001 * ifQuart)

而當入紀年爲 0 時，再減去一個小數就會變為負數，這時蔀序需要取 0。

1 2 3 4 5

if (ifQuart) { BuOrder = Math.max(0, BuOrder) }

若入紀年爲 1520，卽該年入最後一蔀第 20 蔀丁酉蔀 76 年，則規定蔀序號爲 19（第 1 蔀甲子蔀蔀序爲 0）。由於 MOD(1520,76)=MOD(0,76)=0，若不加以規定，結果與入紀年爲 0 時相同，爲甲子蔀 1 年。

1 2 3 4 5

if ((OriginYear % YuanRange == JiRange) && ifQuart) { BuOrder = 19 }

之所以要區分是四分曆還是三統曆，因為三統曆在計算入蔀年時算外，而四分曆算上，所以三統曆不需要像四分曆一樣退一位。

其實四分曆跟三統一樣也是算外。

本程序各曆入蔀年置閏判斷邏輯：

• 建子冬至：13 有 FirstMonNum==0 && WsolsticeOriginMon==0
• 建寅冬至、雨水：12 有 FirstMonNum>0
• 建子雨水：13 無 FirstMonNum==0 && WsolsticeOriginMon!=0

非冬至元積月問題

突然發現非冬至元建子的積月數有問題，不能跟冬至閏年的實際情況相合，我就用了整整一個晚上來做找規律的遊戲。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

   else if (FirstMonNum == 0 && WsolsticeOriginMon != 0) {
        if (ifOriginLeapThisY + ifLeapPrevPrevY == 0) {
            FirstMonAccumMon -= ifLeapThisY
        }  //顓頊：3,6,8,9,10
        if ((ifOriginLeapPrevY + ifLeapThisY + ifLeapPrevPrevY == 0) || (ifOriginLeapPrevY + ifLeapThisY + ifLeapPrevPrevY + ifOriginLeapPrevPrevY == 1)) {  
            FirstMonAccumMon += ifOriginLeapThisY
        }
        else if ((ifOriginLeapPrevY + ifLeapThisY + ifLeapNextY == 0) || (ifOriginLeapPrevY + ifLeapThisY + ifLeapPrevPrevY == 2)) {  
            FirstMonAccumMon += ifOriginLeapNextY
        }
    }

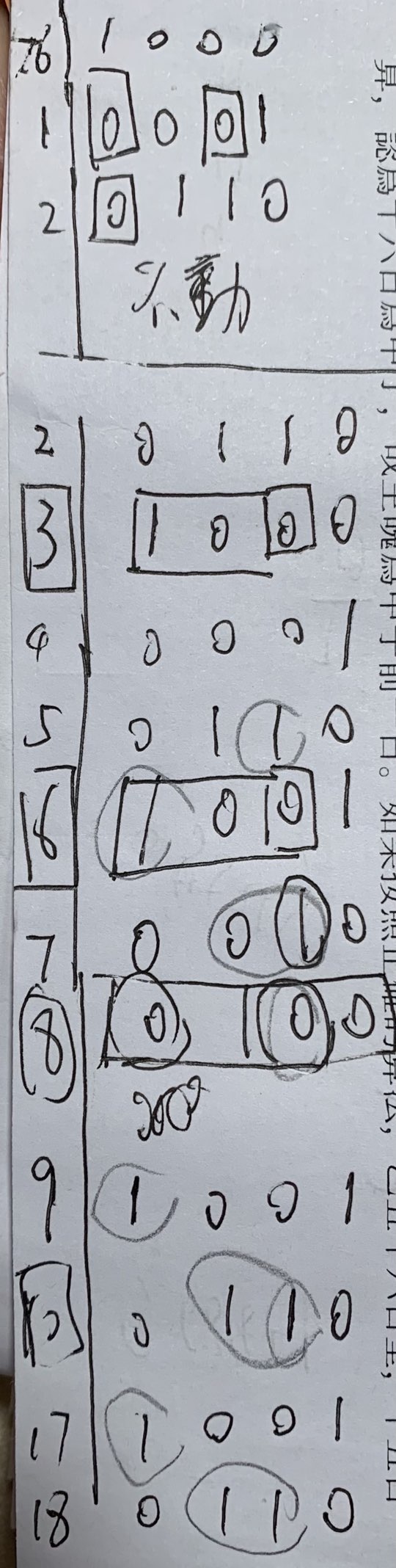
按照上面這樣，按下葫蘆又起瓢，一晚上都沒調整好，還撤掉了不少頭髮。甚至用上了這些變量：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

    var OriginLeapPrevPrevY = (BuYear - 3) * 7 / 19 - Math.floor((BuYear - 3) * 7 / 19)
    var OriginLeapPrevY = (BuYear - 2) * 7 / 19 - Math.floor((BuYear - 2) * 7 / 19)
     var OriginLeapThisY = (BuYear - 1) * 7 / 19 - Math.floor((BuYear - 1) * 7 / 19)
    var OriginLeapNextY = BuYear * 7 / 19 - Math.floor(BuYear * 7 / 19)
    var LeapSurPrevPrevY = (((BuYear - 3) * 7 / 19 - Math.floor((BuYear - 3) * 7 / 19) + WsolsticeOriginMon) % 1 + 1) % 1
    var ifOriginLeapThisY = OriginLeapThisY >= parseFloat((12 / 19).toPrecision(12)) ? 1 : 0
    var ifOriginLeapNextY = OriginLeapNextY >= parseFloat((12 / 19).toPrecision(12)) ? 1 : 0
    var ifLeapPrevPrevY = LeapSurPrevPrevY >= parseFloat((12 / 19).toPrecision(12)) ? 1 : 0
    var ifOriginLeapPrevPrevY = OriginLeapPrevPrevY >= parseFloat((12 / 19).toPrecision(12)) ? 1 : 0
    var ifOriginLeapPrevY = OriginLeapPrevY >= parseFloat((12 / 19).toPrecision(12)) ? 1 : 0

睡了一覺起來，覺得這樣不是辦法，想到應該這樣：

1

var FirstMonAccumMon = Math.floor((BuYear - 1) * 235 / 19 + WsolsticeOriginMon) + FirstMonNum // 正月積月

積月加上一個閏餘修正就完美解決了。真是摸著石頭過河。

此外還有這種麻煩的判斷邏輯：

1

if ((FirstMonNum > 0) && ((WsolsticeOriginMon == 0) || (WsolsticeOriginMon != 0 && ifAdvance == 0) ||(WsolsticeOriginMon != 0 && ifAdvance == 1 && ifLeapThisY==1)  ))

顓頊：

1

var WsolsticeAccumRaw = (BuYear - 1) * solar + WsolsticeOriginDif % 60

之所以中氣置閏出問題，就在於最後 WsolsticeOriginDif 沒有模，導致中氣比朔少 60 天。

授時曆：極端情況：1327 年閏餘 18.3960199417，1328 年閏餘 0.158988062985，1328 年正月和冬至同爲乙丑（建子），所以正月就是閏月，但是不可能閏 0 月，怎麼辦呢？如果遇到閏 0 月，則退到去年的 12 月。1327 當閏不閏。

誤差校驗

• 冬至日期：

  • 公元前 1500 年，授時曆比實曆提前 6 日

  • 前 1140、1000 年提前 4 日

  • 前 500 年提前 2 日

  • 前 100 年提前 1 日

  • 300、800、500、800、1200、1600 年相等

  • 1800 年提前 1 日。

  所以授時曆在大約在公元 300–1600 年是非常準確的。公元前往上，誤差以大約 250–300 年 1 日的速度迅速擴大。這是為什麼呢？誤差為什麼不是線性增長？

• 我自己改了授時曆的回歸年、朔望月、近點月參數，新法在公元前 1500–前 500 年基本與實曆相合。

• 中氣：

  • 公元 1140 年，授時只有一個與曆書平氣相差一天，新法都是對的
  • 300 年，新法基本提前平氣 2 天，授時提前 3 天，冬至新法與定氣相同，授時提前一天。不知是不是當時曆書平氣不太準。
  • 前 722 年，新法比定氣晚 1 日或相同，授時跟殷曆相同或比殷曆提前 1，殷曆比定氣提前 1 或 2

• 至於商代時間，尙書只有伊訓太甲中兩篇僞古文可供討論，再結合世經，將商代年數劃定在公元前 1752–1697（或者 1739）年。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

if (ifLeapAvgThis && !ifLeapAcrThis) {
        var ifLeapAdvanceStartThis = 1
        var ifLeapAdvanceEndThis = 1
    } else if (ifLeapAvgThis && ifLeapAcrThis) {
        var ifLeapAdvanceStartThis = 0
        var ifLeapAdvanceEndThis = 1
    } else {
        var ifLeapAdvanceStartThis = ifLeapAvgThis
        var ifLeapAdvanceEndThis = ifLeapAcrThis
    }

優化後：

1
2

var ifLeapAdvanceStartThis = ifLeapAvgThis && !ifLeapAcrThis
var ifLeapAdvanceEndThis = ifLeapAvgThis || ifLeapAcrThis

說明

比如，雨水元夏曆入蔀 3、4 年：

● 雨夏 2758803 天紀甲子蔀 3 大 18 小 255 冬大 9 雨水 10.5 閏餘 0439 朔 壬午 辛亥 辛巳 庚戌 庚辰 己酉 己卯 戊申 戊寅 戊申 丁丑 丁未 分 2713 8021 3330 8638 3947 9255 4564 9872 5181 0489 5798 1106 望 丁酉 丙寅 丙申 乙丑 乙未 甲子 甲午 癸亥 癸巳 壬戌 壬辰 辛酉 分 0367 5676 0984 6293 1601 6910 2218 7527 2835 8144 3452 8761 中 甲辰 乙亥 乙巳 丙子 丙午 丁丑 丁未 □□ 戊寅 戊申 戊寅 己酉 分 9375 3750 8125 2500 6875 1250 5625 □□ 0000 4375 8750 3125

● 雨夏 2758804 天紀甲子蔀 4 大 12 小 603 冬大 14 雨水 15.75 閏餘 4123 朔 丙子 丙午 乙亥 乙巳 甲戌 甲辰 癸酉 癸卯 壬申 壬寅 辛未 辛丑 分 6415 1723 7032 2340 7649 2957 8266 3574 8883 4191 9500 4809 望 辛卯 庚申 庚寅 己未 己丑 己未 戊子 戊午 丁亥 丁巳 丙戌 丙辰 分 4069 9378 4686 9995 5303 0612 5920 1229 6537 1846 7154 2463 中 己卯 庚戌 庚辰 辛亥 辛巳 辛亥 壬午 壬子 癸未 癸丑 甲申 甲寅 分 7500 1875 6250 0625 5000 9375 3750 8125 2500 6875 1250 5625

4 年的年前冬至是戊寅。

置閏共有三種方法：閏餘法、無中氣法、固定冬至法，閏餘法可分為年中置閏、年末置閏兩種，無中氣法閏月必在年中（當然也可能在最後一個月），固定冬至法閏月必在年末。本表置閏採用閏餘法。第一行最後標注的閏月是閏餘年中置閏法的閏月，若採用閏餘年末置閏法，最後一個月就是閏月。中氣一行採用無中氣置閏法，有「□□」的年份爲無中氣置閏法的閏年，「□□」表示該月無中氣，爲閏月。固定冬至法的閏月必定置於年末，

無中氣法的閏月可能比閏餘年中法提前一個月：中氣與朔同在一日，中氣的時刻比朔早，則閏餘未達到閏準，還不能置閏；但是由於中氣與朔已經在一日了，絕大多數情況下上個月無中氣，需要置閏。

一個需要注意的細節是，如果閏餘法閏年在無中氣法的上年，那麼無中氣法的閏月需要加一，因為本表是按照閏餘法來排的。

隨記

• 中午散步想到西曆其實很迷。眞正的陽曆應該是這樣的：1 月一般 30 有日，1 日爲冬至；2 月一般有 29 日，1 日爲大寒；3 月有 30 日，1 日爲雨水；4 月有 31 日，1 日爲春分；5 月有 31 日，1 日爲穀雨；6 月有 31 日，1 日爲小滿，7 月有 31 日，1 日爲夏至；8 月有 32 日，1 日爲大暑⋯⋯每月的日數爲 29–32 日。壞處就是每月的日數沒那麼規則，需要像中曆一樣每年根據觀測結果來修正。然後看到伊朗曆其實就是這種思路，只是把春分作爲新年。

• 中國應該廢除春節，把新年改成從冬至到元旦的這十天。這樣旣符合傳統中歷的眞正新年，又能與公曆元旦接軌，又能與聖誕節接軌，不會與世界主流經濟作息錯開。

• 1 月 15 日：同學給我發了張照片，我看到月亮輪廓，說目測今天初三，一看日曆果然初三。這就是朏啊。

• 1 月 16 日：今天的月亮依然很细，但已经初四了。所以初三的更细，初二应该细到几乎不可见。

• 在線繪製函數圖像

• 朱桂昌曆表後記的刊誤：顓頊日曆表第 528 頁元封七年四月二十九日應爲庚申，誤爲癸申。太初日曆表第 470、472 頁標題應爲神爵元年、神爵二年。

• 由於三統曆之後都採用無中氣置閏，所以不用考慮閏餘今年和明年的問題，因為無中氣都是看今年閏餘。

• 《後漢·律曆志下》：

  太初曆到章帝元和，旋復疏闊，徵能術者課校諸曆，定朔稽元，追漢（三）〔四〕十五年庚辰之歲，追朔一日，乃與天合，以爲四分曆元。加六百五元一紀，上得庚申。有近於緯，而歲不攝提，以辨曆者得開其説，而其元尠與緯同，同則或不得於天。

  得《後漢四分曆》上元積年 605*4560+1520=2760320，爲公元前 -160-2760320=-2760480