幾何
會圓術
會圓術求法:半弦長 c = sqrt (r^2 - (r-h)^2)。尤其需要注意的是,會圓術的標準是週天度 365.25,直徑 121.75,卽「週三徑一」,這箇單位系是以 3 爲標準,而非圓周率 π
傅宗

弧矢割圓術
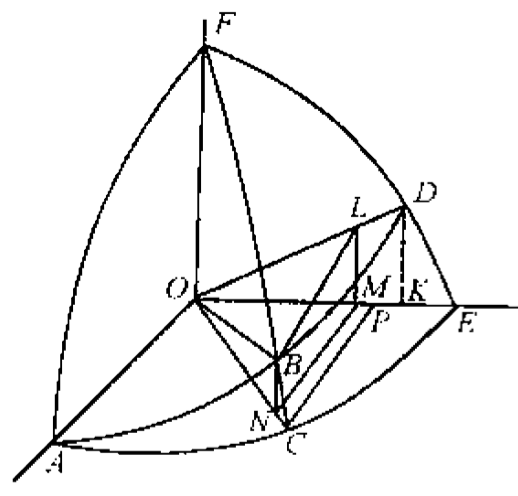
圖
授時只有黃度轉赤度的方法,我另外推導出了赤度轉黃度的方法:從 C 向上作垂線,與 OB 相較於點 T,T 超出了球體。從 P 向上作垂線,交 OD 於 Q。有了這兩條輔助線,就可以從赤轉黃了。
大衍術
大衍求一術
解一次同餘式的核心模塊,孫子定理、不定方程、調日法、演紀都需要求一術。輸入兩箇互質整數a * x ≡ 1 (mod b) 的解 x
大衍總數術
卽解同餘式組,是秦九韶推廣之孫子定理。求解多組 x ≡ ri (mod mi) ,有解的充要條件是 gcd (mi, mi+1) | abs (ri - r i+1);依次輸入各組餘數 r、元數 m。孫子定理有解的充要條件:(m1,m2 | |r1-r2|) 1、定母 i|元數 i;2、定母互質;3、M=定母相乘=元數的最小公倍數。在孫子定理中,模數需兩兩互質,而秦九韶將不互質的元數變爲互質的定母,進而可以使用孫子定理求解。
連分數
給定一箇分數,求其連分數、各漸進連分數。非常適合與調日法參照。古代數學似乎沒有小數,都是分數運算,而計算機程序都是浮點運算,所以也可以用這箇工具將計算機計算出的結果轉換爲分數。
調日法
一箇朔望月是 29.53059 日有餘,在朔餘 / 日法 可表示爲 (26m+9n) / (49m+17n) ,m 卽陽率
無窮調日法是我自己的一點點小改進。彊弱率需滿足如下條件: ,卽
,卽 彊子 * 弱母 - 彊母 * 弱子 = 1 。那麼推廣開來,26/47 和 9/17 只是一種可能性而已,適合求朔分 0.5305 附近的數,而任何滿足這箇條件的彊弱二率,都可以用來調制。只需要輸入分母弱數 < 彊母,例如玄始曆 47251 / 89052,李銳公式解得 47252 = 26×1816 + 9×4,累強弱、顧-陳公式解得 47251 = 26×1799 + 9×53,卽 47251 / 89052 和 47252 / 89052 都滿足調日法,但李銳公式求不出前者。
宋
自漢太初至于今,冬至差十日,如劉歆三統復強於古,故先儒謂之最疏。後漢劉洪考驗四分,於天不合,乃減朔餘,苟合時用。自是已降,率意加減,以造日法。宋世何承天更以四十九分之二十六爲強率,十七分之九爲弱率,於強弱之際以求日法。承天日法七百五十二,得一十五強,一弱。自後治曆者,莫不因承天法,累強弱之數,皆不悟日月有自然合會之數。
今稍悟其失,定新曆以三萬九千爲日法,六百二十四萬爲度母,九千五百爲斗分,二萬六百九十三爲朔餘,可以上𥡴於古,下驗於今,反覆推求,若應繩準。又以二百三十萬一千爲月行之餘
月行十三度之餘 ,以一百六十萬四百四十七爲日行之餘日行周天之餘 。乃會日月之行,以盈不足平之,幷盈不足,是爲一朔之法日法也,名元法 。今乃以大月乘不足之數,以小月乘盈行之分,平而幷之,是爲一朔之實周天分也 。以法約實,得日月相會之數,皆以等數約之,悉得今有之數盈爲朔虛,不足爲朔餘 。又二法相乘爲本母,各母互乘,以減周天,餘則歲差生焉,亦以等數約之,卽得歲差、度母、周天實用之數。此之一法,理極幽眇,所謂反覆相求,潛遁相通,數有冥符,法有偶會,古曆家皆所未達以等數約之,得三萬九千爲元法,九千五百爲斗分,二萬六百九十三爲朔餘,六百二十四萬爲日度母,二十二億七千九百二十萬四百四十七爲周天分,八萬四百四十七爲歲差 。上 宋志七
以下是各曆朔餘、日法:
| |
累強弱法剛寫出來的時候把各曆都算了一遍,上面是當時的情況,發現欽天以後大量朔餘用累強弱之數法算不出來。後來寫了分解公因數程序,突然發現這些求不出來的全都是可以通分的,通分之後就都求出來了!看來宋曆的 朔餘 / 日法 還照顧了其他因素。而李銳公式求不出的,我通分之後依然求不出。
三統 遠超強率 26/49,但另有方法。用連分數逼近,求得各漸進分數: (1) 0/1 (2) 1/1 (3) 1/2 (4) 8/15 (5) 9/17 (6) 17/32 (7) 43/81,其中 17/32 大於 43/81,可以作爲強率,於是弱率爲 9/17。算調日法,得 43 = 17×2 + 9×1,81 = 32×2 + 17×1,2 彊 1 弱。可是這樣就算調出來了也毫無意義,因爲三統是以律起曆用三分損益率構造日法 ,當然跟調日法毫無關係。- 同理,
四分曆 各漸進分數: (1) 0/1 (2) 1/1 (3) 1/2 (4) 8/15 (5) 9/17 (6) 17/32 (7) 26/49 (8) 43/81 (9) 499/940,因此可以用三統 43/81 作爲強率,弱率得 26/49,得 11 強 1 弱。四分曆也可以調出來,同樣,毫無意義。 大象曆 也超過了強率。劉洪濤認爲,大象 是以四分曆 499/940 爲強率,以何承天 9/17 爲弱率,得(499*1107 + 9*11257)/(940*1107 + 17* 11257) = 28422/53563。古代曆法計算法 頁 617統天 超過強率,按照調日法求出來是 6367,多出來的 1 是留給朔實消長的空間。開禧 以弱換強:16900=169*49+507*17=339*49+17*17=(169+17*10)*49+(507-49*10)*17乾道 用李銳公式算出來的是以弱換強之後的,但數學上我不太懂,以弱換強的話,日法都是一樣的,爲何朔餘就不一樣了?
垛積術
「垛積」卽等差級數求和。
隙積術 芻童垛
「芻童」卽長方稜臺。上有寬 a 箇、長 b 箇,下有寬 c 箇、長 d 箇,共 n 層,每層長寬各多 1 箇。

四角垛 方垛
卽自然數平方級數求和。1+4+9+...+n^2 = 1/3 n (n+1) (n+1/2)=1/6 n (n+1) (2n+1)
三角垛 落一形垛
源於七乘方圖。p = 2 時,1+3+6+10+...+n (n+1) /2 = 1/6 n (n+1) (n+2)。通項公式:1/(p+1)! n (n+1) (n+2) ... (n+p)
招差術
一箇 p 次多項式可表爲一箇 p 次內插公式;以 p 次多項式爲通項的 p 階等差數列的和是一箇 p+1 次多項式。招差術的實質是將高階等差數列的通項多項式表爲內插公式。招差的差系由給定的數列求得,內插的差系由數列的和函數求得。
參考資料
這個網站是古代曆法研究者的共同智慧結晶,在此表示感謝
天學章
- 點擊下載鄭慧生
認星識曆——古代天文曆法初步 河南大學出版社,2006 秊 的 星圖我按歲星的旋轉順序排的。注意:星圖是左東右西。 - 徐振濤、蔣窈窕
五行聚合與夏商周秊代硏究 北亰:世界圖書出版公司,2006 秊 可作爲入門導讀。不過這麼水的書都能筭斷代工程…… - 古代曆法 的書
- 敎材
自然地理學 - 知乎。維基百科。
古籍
- 各史曆志
- 開元占經
- 寶祐四年會天曆
- 馮立昇主編
疇人傳合編校注 ,中州古籍,2012 - 鄧文寬
敦煌天文曆法文獻輯校 - 梅文鼎
梅氏叢書輯要 - 李銳
李氏遺書 - 李亮等編
海外珍稀中國科學技術典籍集成 ,2010
專書、論文集
- 劉洪濤
古代曆法計算法 - 張培瑜等
中國古代曆法 - 陳美東
古曆新探 - 陳美東
中國科學技術史稿 頁 106 - 曲安京
中國曆法與數學 - 曲安京
中國數理天文學 秦九韶與數書九章
古曆的計算機模擬
目前發現了三篇博士論文:
- 邢钢
中国早期历法的计算机模拟分析与综合研究 ,中國科學技術大學博士論文,2005 年 - 李亮
明代历法的计算机模拟分析与综合研究 ,中國科學技術大學博士論文,2011 年 - 滕艳辉
宋代朔闰与交食研究 ,西北大學博士論文,2012 年
論文
躔離氣朔
- 陈美东:日躔表之研究
- 陈美东:月离表初探
- 徐传胜:
乾象历 月离表数理分析 - 尚晓清:
大衍历 定朔算法及程序说明 - 滕艳辉:
纪元历 定朔算法模型及分析 - 滕艳辉等:
纪元历 等 8 部宋代历法的定朔推步及精度分析 - 马莉萍:中国古代历法中合朔时的太阳位置
- 王荣彬:中国古代历法的中心差算式之造术原理
- 李勇:中国古历定朔推步综述
- 李勇:中国古历经朔数据的恢复及应用
- 滕艳辉:宋代历法中的置闰算法
- 李勇:明嘉靖六年
大统历 历书的气朔推步精度 - 滕艳辉:统天历的岁实消长与气朔算法分析
- 刘娅娅:朱载堉对授时历岁余计算的检验与修正
- 张祺:梅文鼎和江永的回归年消长法
天文計算
- 陈美东:中国古代有关历表及其算法的公式化
- 王锦瑞:
明天历 岁差与上元积年 - 陈美东:中国古代太阳视赤纬计算法
- 江晓原:中国古代对太阳位置的测定和推算
- 陈美东:中国古代昼夜漏刻长度的计算法
- 纪志刚:麟德历晷影计算方法研究
- 陈美东:中国古代月亮极黄纬计算法
- 陈久金:九道术解
- 周靖:月行九道考
- 曲安京:
授时历 的白赤道坐标变换法
交食
- 刘金沂:隋唐历法中入交定日术的几何解释
- 滕艳辉:
戊寅元历 的日月食推算方法 - 刘金沂:麟德历交食计算法
- 滕艳辉:
崇天历 的日食推步术 - 袁敏:
明天历 日食算法分析 - 滕艳辉:
纪元历 日食算法及精度分析 - 李勇:
授时历 交食推步研究 - 唐泉:
授时历 和回回历法 中的日食时差算法 - 李勇:授時曆與仲康日食推算
- 李勇:中国元明时期交食推步的比较研究
- 陈美东:中国古代的月食食限及食分计算法
- 曲安京:中国古代日食食限与食分算法
- 滕艳辉:宋代的日食食限算法
- 曲安京:中国古代的日食时差算法
- 唐泉:中国古代的日食食分算法
- 曲安京:中国古代的月食时差算法
- 李鉴澄:中国历代日月交食周期的研究
- 马莉萍:中国古代交食的宿度记录及其算法
曆法數學
- 陈久金:调日法研究
- 李继闵:关于调日法的数学原理
- 刘钝:李锐顾观光调日法工作述评
- 李继闵:再评清代学者的调日法研究
- 曲安京:中国古代的二次求根公式与反函数
- 曲安京:唐宋历法演纪上元实例及算法分析
- 曲安京:东汉到刘宋时期历法上元积年计算
- 王翼勋:开禧历上元积年的计算
- 王翼勋:秦九韶演纪积年法初探
- 王锦瑞:
明天历 天文常数系统中的缺陷解析
招差術
- 李兆华:朱世杰招差术探原
- 李兆华:朱世杰的垛积术与四次内插法
- 李兆华:
平立定三差详说 的一点注记 - 曲安京:
皇极历 中的漏刻差分表 - 刘钝:
皇极历 中等间距二次插值方法术文释义及其物理意义 - 武家璧:
大衍历 日躔表的数学结构及其内插法 - 曲安京:
大衍历 晷影差分表的重构 - 王荣彬:中国古代历法三次差插值法的造术原理
- 陈美东:
崇玄 仪天 崇天 三历晷长计算法及三次差内插法的应用
普通曆法
- 刘次沅:
史记历术甲子篇 探讨 - 武家璧:包山楚简的岁首占及其历朔断代
- 武家璧:简论楚《颛顼历》
- 严敦杰:补北齐书历志
- 黃一農:中國史曆表朔閏訂正舉隅–以唐麟德曆行用時期爲例
- 劉金沂:李淳風的曆象志和乙巳元曆
- 钮卫星:符天历历元问题再研究
- 陈久金:符天历研究
- 孔庆典:七元甲子术研究
- 陈久金:回人马依泽对宋初天文学的贡献
- 邱靖嘉:
遼史曆象志 溯源——兼評晚清以來傳統曆譜的系統性缺陷 - 邱靖嘉:
辽史 所见祖冲之大明历 的文献价值发覆 - 郭津嵩:撒馬爾干的中國曆法——耶律楚材的西征庚午元曆及其里差法考辨
具注曆
- 李勇:中国古历中的步发敛
- 朱双双:中国古历没灭术研究
- 何啓龍:
授時曆 具注曆日原貌考 - 金身佳:敦煌写本宅经 P.3594 九方色图试释
- 宁宇:敦煌写本时日宜忌文书之思想主题探赜
- 邓文宽:敦煌古历丛识
- 邓文宽:敦煌文献 S2620 号唐年神方位图试释
- 華瀾:敦煌曆日探研
- 邓文宽:跋吐鲁番文书中的两件唐历
- 何伟凤:黑水城出土元代历日研究
數學
- 甘向阳:
九章算术 刘徽注中的算法分析工作与算法分析思想 - 陈巍:
五经算术 的知识谱系初探 - 沈康身:
数书九章 大衍类算题中的数论命题 - 汪晓勤:
数书九章 大衍类算题的若干注记 - 一次同余式组的程序求解
- 陈维海:用 BASIC 程序实现求高次方程实根的斯特姆秦九韶方法
- 朱一文:秦九韶「历家虽用用而不知」解
- 侯钢:秦九韶大衍总数术中问数化定数算法解析
- 王翼勋:从大衍术到大衍求一术
- 段耀勇:刘徽开方与增乘开方法
- 梅荣照:贾宪的增乘开方法_高次方程数值解的关键一步
- 李兆华:增乘开方法与贾宪三角形
- 傅宗:隙积术和会圆术——沈括
梦溪笔谈 评注一则
現代天文
- 李文:地球椭球模型中太阳位置计算的改进
- 张富、张丽娟、邱本志:一种计算太阳低仰角蒙气差的有理函数逼近方法
- 丁豔、袁隆基、趙培濤、仝軍令:太陽視日軌跡跟蹤算法研究