律曆初階下｜三：天文計算

『月行正交入夏至後宿度內爲同名，入冬至後宿度內爲異名

槪念

基本名詞

• 歲實 回歸年。不同時期大約長度：四分曆 365.25，魏晉系 365.246，唐系 365.244– .245，宋系 365.243 – .244，授時 365.2425。
• 週天 恆星年，祖沖之大明將歲差引入曆法約 45 年差 1 度，誤差較大，李淳風麟德不用歲差，此後一直沿用大約 70 餘年差 1 度。
• 月 一箇朔望月一般在 29.53059–29.5306 日之間。日法：朔望月分母，從李淳風麟德開始用總法，所有參數的分母都是日法。
• 轉 曆 變 與近點月約 27.5545 日有關，「入轉日」卽在一箇近點月中的日數。有 8 部曆法以遠地點月速最慢入轉，其餘都是近地點月速最快入轉。魏晉南北曆法的「曆」指與近點月相關的參數，「曆法」卽近點月長度。
• 交 與交點月 約 27.2122 日有關，「入交日」卽在一箇交點月中的日數。升交點卽「正交」，降交點稱「中交」，兩箇交點之間稱「半交」。降交點到升交點，月在黃道南，稱「陽曆」「陽道」「外道」；升交點到降交點，月在黃道北，稱「陰曆」「陰道」「內道」，所以看到「陰陽曆」的說法，不要與現在說的陰陽曆混淆了。起於降交點的只有景初、開皇、統天三曆。若起於降交點，則正交爲降交點，其他大部分都是升交點。
• 日躔 月離 指日月運行。日月都是在近地點最快，遠地點最慢。
• 赤道積度 黃道積度 赤道經度，黃道經度。古代天文模型與現代天文學不同，黃經不是現代意義上的黃經，而是黃道與赤經圈相交得到的黃道度數，可稱爲「極黃經」，同樣，白經其實是「極白經」。太陽在黃道上運行，因此太陽的極黃經與黃經相等。積度與宿度不一樣。
• 月道 白道 授時曆開始纔稱白道，此前都直說月道，白道是月行九道詳見下中的一道。
• 內外度 緯度。黃道內外度卽黃緯，赤道內外度卽赤緯。 去極度 象限度 - 內外度 = 去極度，卽到天頂的距離。
• 昏旦中星 昏明時刻正南的星宿。

數學術語

• 古筭分子稱實，分母稱法。筭外：不筭第一秊，筭上：筭第一秊。日如第一秊第二秊第三秊，筭外兩秊，筭上三秊。「%」表示模，卽取餘數，9 % 4 = 1，這樣方便許多。

• 看到減的時候要留意誰減誰。某甲「反減」「覆減」乙的意思是 乙 - 甲。「相減」默認就是以大減小

• 「進二位」「進二等」意思是 × 100，「退位」指 / 10

• 應天曆的「身外除一」「身外除三」不懂什麼意思

• 「因」同「乘」

• 「甲少於乙 10 已下」意思是 甲 >= 乙 - 10，同理，「甲少於乙 10 已上」意思是 甲 <= 乙 - 10

• 唐宋食分都是用太半少來表示，麟德：「餘半以下，爲半弱；半以上，爲半強。」

  0–0.25	0.25–0.5	0.5–0.75	0.75–1
  某	某度少或半弱	某度半	某度太或半強

  觀天：「其分就近約之爲太、半、少。」少半太是 0.25-0.5-0.75，旣然是就近，那似乎可以理解爲 0–0.125 爲某度，0.125–0.375 爲某度少，0.375–0.625 爲某度半，0.625–0.875 爲某度太，0.875–1 爲某 +1 度。在時間模塊有相應轉換工具。

天文術語

• 積年 * 回歸年 =【庚午】通積分

• 距冬至日數 = 【崇天】中積 = 【明天】中日

• 黃道月道同名異名十分迷惑：

  • 五紀「凡春分後陰曆交後，秋分後陽曆交後，爲月道同名，餘皆爲異名。」似乎說只有交後纔算同名，則同名只有四分之一的情況。又說「月道同名者，交前爲加，交後爲減；異名者，交前爲減，交後爲加。」則同名異名皆有交前交後。
  • 觀天：「凡日以赤道內爲陰，外爲陽；月以黃道內爲陰，外爲陽。故月行宿度，入春分，交後行陰曆，秋分，交後行陽曆——皆爲同名；入春分，交後行陽曆，秋分，交後行陰曆——皆爲異名。」
  • 紀元、重修大明：「月行正交入夏至後宿度，內爲同名，入冬至後宿度，內爲異名。⋯⋯其在同名者，⋯⋯半交後，正交前，以差減；正交後，半交前，以差加。」原本的句讀是「入夏至後宿度內爲同名」，我覺得應該斷開。這裏的正交應該指兩箇升降交點，半交指四分之一交點月，則同名旣有交前又有交後。

  還是觀天說得最清楚，暫時統一按觀天處理：秋分到次年春分太陽在陽曆，春分到秋分太陽在陰曆，交初到交中月亮在陽曆，交中到交初月亮在陰曆。觀天只舉交後而言，但交前交後照理說都一樣的，否則春分交前陰曆之類就旣不同名也不異名。

• 交前交後也容易混淆。唐宋曆的「交前」卽在交點之前，「交後」卽在交點之後。而隋以前一般用「先交」「後交」。戊寅：「如望差已下，爲去先交分。交限已上，以減交分，餘爲去後交分。」去先交 = 先交 = 交後，去後交 = 後交 = 交前。

• 「去交度乘數除數」只在以下幾部唐曆見過。乘上日法，發現崇玄又和其他幾箇不合。

  • 大衍 3040 * 11/2643 = 12.6523
  • 五紀交度乘數十一，除數千一百六十五 1340 * 11/1165 = 12.6523
  • 正元 1095 * 11/945 = 12.746，應該沒問題，如果要跟其他接近的話就改成 1095 * 11/952 = 12.6523
  • 宣明去交度乘數十一，除數七千三百三 8400 * 11/7303 = 12.6523
  • 崇玄去交度乘數十一，除數八千六百三十二 13500 * 11/8632 = 17.203429，改成 13500 * 11/11632 = 12.7665，13500 * 11/11732 = 12.6577，13500 * 11/11737 = 12/6523

  大衍云「大抵去交十三度已上，雖入蝕限，爲涉交數微，光景相接，或不見蝕。」看來唯一的作用就是用來判斷是否超出 13 度⋯⋯這箇値是 1.028 日。這無關緊要，我們只需要根據日分來計算卽可。

• 「無同率」。大衍入氣差積有一句「其二至之前一氣，皆後無同差，不可相并，各因前末爲初率。」其他地方還有「其後無同率」。例如 [10, 13, 13, 10] ，前後都是 13，所以相互之間沒有差，這時就要減去前面的 10 來作爲差。

歲

歲差

現代歲差常數是 0.014162 度/年。

大衍曆議論歲差：新唐志卷二十七上

大同九年543，虞𠠎等議：

姜岌、何承天俱以月蝕衝步日所在。承天雖移岌三度，然其冬至亦上岌三日。承天在斗十三四度，而岌在斗十七度，其實非移。祖沖之謂爲實差，以推今冬至，日在斗九度算得大明推 543 年冬至在斗 9.2，用求中星不合。自岌至今，將二百年，而冬至在斗十二度。然日之所在難知，驗以中星，則漏刻不定。漢世課昏明中星，爲法已淺。今候夜半中星，以求日衝，近於得密。而水有清濁，壺有增減，或積塵所擁，故漏有遲疾。臣等頻夜候中星，而前後相差或至三度。大畧冬至遠不過斗十四度，近不出十度。

又以九年三月十五日夜半，月在房四度蝕。九月十五日夜半，月在昴三度蝕。以其衝計，冬至皆在斗十二度。自姜岌、何承天所測，下及大同，日已却差二度。而淳風以爲晉、宋以來三百餘歲，以月蝕衝考之，固在斗十三四度間——非矣。

劉孝孫甲子元歷（孝孫A）推太初前 104冬至在牽牛初；下及晉太元、宋元嘉，皆在斗十七度；開皇十四年594，在斗十三度。而《劉焯歷》仁壽四年605冬至，日在黃道斗十度，於赤道斗十一度也。其後孝孫改從焯法（稱孝孫B），而仁壽四年冬至，日亦在斗十度。焯卒後，冑玄以其前歷上元起虛五度（姑且命名為大業A），推漢太初，猶不及牽牛，乃更起虛七度（命名為大業B），故太初在斗二十三度，永平在斗二十一度，並與今歷合。而仁壽四年605，冬至在斗十三度，以驗近事，又不逮其前歷矣。戊寅歷，太初元年辛酉冬至（我算得壬戌0331，差了一點），進及甲子（為何要看甲子？），日在牽牛三度。永平十一年（68 年）得戊午冬至（我算得戊午8616），進及辛酉，在斗二十六度。至元嘉（424 年）中，氣上景初三日（戊寅曆乙丑9432，景初曆丁卯7965，應該是「上二日」），而冬至猶在斗十七度。欲以求合，反更失之。又曲循孝孫之論，而不知孝孫已變從皇極，故爲淳風等所駁。歲差之術，由此不行。

⋯⋯又皇極歷歲差皆自黃道命之，其每歲周分，常當南至之軌，與赤道相較，所減尤多。計黃道差三十六度，赤道差四十餘度，雖每歲遯之，不足爲過。然立法之體，宜盡其原，是以開元歷皆自赤道推之，乃以今有術從變黃道。

虞𠠎測出當時冬至在斗 10–14 之間，誤差的原因是漏壺精度。根據兩次觀測結果，冬至都在 12 度。

下表各年第一行是一行的計算，第二行為我的計算。

還是不理解「欲以求合，反更失之」是要合誰。

歲實消長

由於地球自轉放慢等因素，回歸年會逐漸變短，現代値大約是 365.24218968 - 6.16*1e-8 * (year - 2000)，按照等差數列求和，歲實消長的累積値就是 (0 + 6.16*1e-8 * (y - 2000)) * (y - 2000) / 2 = 3.08 * 1e-8 * (y - 2000)^2

統天發明歲實消長，授時繼之。統天百年減 2.1167 分滕艳辉、王鹏云、刘娅娅 统天历的岁实消长与气朔算法分析，比實際高了 36 倍，這樣三百年下來就有一刻的誤差了。統天有歲實消長、朔實消長，授時只有歲實消長，按照授時術文，加上歲實消長後只有冬至時間會變化，經朔時間毫無變化。授時百年減 1 分，歲實大約是百年減 2 分，比統天小了一些，還是比實際高 32 倍，這樣四百年誤差一刻，此後誤差加速增大。

朱載堉聖壽萬年曆：「新法不及二秒，而歲週氣策等率皆活法，以其每年增損無定，故不開列，各隨歲差求而用之，與彼二家頗不同也。」說明在當年計算中，統天、授時用的是原本的歲實 .2425，而不用消長後的歲實。

古曆的歲實變化

此二曆的歲實消長是根據以往所有曆法的參數歸算出來的。我們把乾象以後的 55 部曆法按照這樣全部計算一遍：(0.2425 - 斗分) / ((1281 - 制曆年) / 100)，得出每百年消長數，最後求平均值，算出 -0.0005841，卽每百年減 5.8 分。顯然，古曆的回歸年都比實際偏大很多，這是爲了推算古代天象，預留了一些增量。可是增加得太多了，眞的會準確嗎？這是各曆制曆時間與斗分：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

[206, 0.24617996604416703, "乾象"], 
[237, 0.24688008681499696, "景初"], 
[274, 0.246666666666667, "正曆 (擬)"], 
[352, 0.24677452385827792, "通曆 (擬)"], 
[384, 0.24683802529580134, "三紀"], 
[412, 0.2443055555555702, "玄始 (擬)"], 
[443, 0.2467105263157805, "元嘉"], 
[463, 0.24281481856627352, "大明"], 
[522, 0.24372937293730956, "正光"], 
[535, 0.24437096122778712, "明克讓 (擬大同代)"], 
[540, 0.24418742586004782, "興和"], 
[550, 0.2445900253592299, "天保"], 
[566, 0.24428815004262106, "天和 (擬)"], 
[573, 0.2443146514228829, "劉孝孫 (擬)"], 
[576, 0.2442690333530777, "張孟賓 (擬)"], 
[576, 0.24447130450352006, "甲寅 (擬)"], 
[579, 0.24376539408865483, "大象 (擬)"], 
[584, 0.24342463092460775, "開皇 (擬)"], 
[604, 0.243034709193239, "大業"], 
[608, 0.2445437784066371, "皇極"], 
[626, 0.24461115807270062, "戊寅"], 
[626, 0.24461115807270062, "戊寅 (平朔)"], 
[664, 0.24477611940295674, "麟德"], 
[664, 0.24477611940295674, "麟德 (進朔)"], 
[724, 0.24440789473686664, "大衍"], 
[762, 0.24477611940295674, "五紀"], 
[784, 0.24474885844750816, "正元"], 
[822, 0.24464285714287826, "宣明"], 
[892, 0.24451851851853235, "崇玄"], 
[956, 0.2445, "欽天"], 
[962, 0.24445110977802642, "應天"], 
[981, 0.24489795918367463, "乾元"], 
[995, 0.24466477809255593, "至道甲 (擬)"], 
[995, 0.244705882352946, "至道乙 (擬)"], 
[1001, 0.24455445544555232, "儀天"], 
[1021, 0.24450549450551762, "乾興 (擬)"], 
[1024, 0.24457034938620836, "崇天"], 
[1063, 0.24358974358972318, "明天"], 
[1074, 0.2435864978903055, "奉元 (擬)"], 
[1092, 0.24355777223610175, "觀天"], 
[1103, 0.24358974358972318, "占天 (擬)"], 
[1100, 0.24362139917695913, "紀元"], 
[1127, 0.24359464627150373, "楊級大明 (擬)"], 
[1135, 0.243578643578644, "統元"], 
[1167, 0.2436, "乾道"], 
[1176, 0.24361702127657736, "淳熙"],
[1180, 0.24359464627150373, "重修大明"], 
[1180, 0.24359594006767793, "乙未 (擬)"], 
[1191, 0.24372093023254138, "會元"], 
[1207, 0.24307692307689877, "開禧"], 
[1250, 0.2427762039660024, "淳祐 (擬)"], 
[1253, 0.2429158110883236, "會天 (擬)"], 
[1271, 0.242722371967659, "成天"], 
[1220, 0.24359464627150373, "庚午"]

祖沖之大明簡直是一股清流，是統天以前的最佳值，463 年的理論値是 .2422843592，只多了 40 多秒。可見祖沖之完完全全是根據實測確定斗分。

日躔月離

月平行速

月平行速 V 平 = Sidereal/Lunar + 1 。為什麼要加 1？因為是朔望月，每個月要比恆星月多走一點，所以一年下來月亮多走了正好一圈，因為地球也公轉了一圈。v = s / t，總路程是一年走的圈數，一個月走一圈，所以就是一年的月數 +1，時間當然就是一年。

所以可以推出 恆星月 = Sidereal/V平 = Sidereal * Lunar / (Sidereal + Lunar) 。古曆從沒有恆星月，可能確實沒什麼用。

槪念、符號

太陽運動很簡單，週期項影響不大，用一次傅立葉函數就能比較準確地擬合，但有一箇問題是，基本上所有的古曆都以冬至爲近日點日速最快，實際上並不是這麼回事，在 1250 年左右纔是正好以冬至爲近日點，往前往後誤差都會越來越大，只有儀天曆對日躔表有意識地做出了修正。月亮運動相當複雜，週期項非常多，而古曆都僅僅以一箇近點月爲週期，我們只能用非常粗糙的近似修正來模擬古曆模型，這也是一箇一次傅立葉函數。

表格各欄依次爲：

• 日盈縮積，距冬至日數這麼多天，太陽實際上走了多少度
• 月遲疾積，入近點月這麼多天，月亮實際走了多少度
• 日行改正 = 日盈縮積 / (月實行速 - 日實行速)
• 月行改正 = -月遲疾積 / (月實行速 - 日實行速)

平朔 + 日行改正 + 月行改正 = 定朔，平氣 - 日盈縮積 = 定氣，入交定分 = 入交泛分 + 太陽改正 + 0.078507*月亮改正。

自乾象始有月行遲疾，自大業始有日行盈縮，月離表、日躔表卽用來記錄每日、每氣的日月實行情況。表格的數據是離散的，所以要用內插法來計算特定時刻的日月實行。自乾象到大業、戊寅皆用線性內插，皇極始用二次差內插，到授時用三次公式。

• 隋志中說張賔開皇「減朓就朒」，我猜「朓朒」「朏朒」一詞就是張賔開始用的，隨後劉焯皇極沿用，成爲盈縮積的替代說法。晦而月見西方謂之朓，朔而月見東方謂之朒。

古代沒有負數運算的槪念，所以遇到負數都要轉換爲正數，朓朒的正負問題詳見張培瑜等中國古代曆法470 頁。但是要區別對待不同曆法的正負問題非常麻煩，所以我程序中所有曆法的正負都是這樣的：

依次爲：盈縮積、實行速、損益率、列差圖很不精確，只是意思意思。

另外，「四七日」指的是近點月中 6.8886、13.7772、20.6656、27.5545 這四箇七日向上取整，這四點是轉折點，當日損益率需要分段處理皇極、欽天處理爲 6 8/9, 13 7/9, 20 6/9, 27 5/9。有箇標點本斷爲「四、七日」，哈哈。

另外，平朔一般稱「經朔」，欽天稱「常朔」，庚午稱「中朔」。

分母

精確的日月改正算法是：(日盈縮積 - 月朓朒積) / (月實行速 - 日實行速) 。這其實是一箇簡單的 t = v / s 問題，不用考慮符號正負。古曆日月改正的算法可以統一爲這樣加〔六角括號〕的是不同曆法或有或無：

1. 日盈縮積或月朓朒積 = 整日朓朒積 + 該日損益率 * 比例
2. 月實行速 = 整日月實行速 + 〔列差*比例〕
3. 改正數 = (〔日盈縮積〕- 月朓朒積) / (月實行速或月平行速 - 〔日平行速〕)

理想的分母是 月實行速 - 日實行速，但是不同時期的曆法所選分母各不相同，魏晉曆法基本上是 月實行速 - 日平行速，北系是 月平行速，大業是 月實行 - 日平行，隋唐宋系反而退步，都是 月平行，授時曆 月實行。另可見中國古代曆法第 434 頁

後來突然想到，之所以分母要用 月平行速，而不用 月平行 - 日平行，是因爲古曆太陽改正都比實際偏大許多，分母更大的話能夠抵消一部分誤差。各曆太陽朏朒極值：麟德 2.767，大衍降到 2.42，此後一直在 2.4–2.42 之間，南宋後期會元達到最低的 2.3，後來三部南宋曆是 2.36，授時又返回 2.4，而實際上只有 1.98。若用這樣的比例抵銷，2.14 * 12.36875/13.36875 = 1.98，最常見的 2.4 等於 2.22。所以看起來唐以後相比魏晉退步了，但實際效果應該相差不多。

線性還是二次？

崇天日躔：

求經朔弦望入氣朏朒定數：各以所入氣小餘乘其日損益率，如樞法而一，卽得。

明確說「其日」，則是二次插值。每部曆法都會根據日躔術和二十四節氣表編製全年每日的立成表，這就是「其日」的意思，在具體編製每年曆書時只用査立成表進行線性內差卽可，但曆志中無一保存了唐宋曆的立成表，只能自己根據日躔術來寫程序。各曆二次插值具體形式有所不同。對於皇極二次公式，劉鈍皇極曆中等間距二次插值方法術文釋義及其物理意義、曲安京曆法頁 240有不同理解。原文「前少者⋯⋯乃別差加之」，劉鈍改爲「半別差減之」，而「前多者，卽以總差加末率」，劉鈍補上「半別差減之」；曲安京則完全未改動原文，指出這是皇極的失誤之處。結合皇極其他三種二次插值術求月朔弦望應平會日所入遲速、推朔弦望定日術、求月入交去日道來看，劉鈍校改之後的纔是術文原貌。對於崇玄，曲安京說原文是「日差」，但可能是「半日差」之誤。王榮彬認爲儀天、崇玄完全一致王榮彬中國古代曆法的中心差算式之造術原理，而崇玄又與崇天完全一致曲安京曆法頁 241。以上觀之，日躔等間距二次差公式有這四種形式：

符號：Δ1 爲本氣升降分、損益率，Δ2 爲後氣升降分、損益率，(Δ1-Δ2) / n 是總差、合差、差率，(Δ1 - Δ2) / n^2 是別差、日差。

1. 麟德：氣初日消息數 (Δ1+Δ2)/2n + (Δ1-Δ2)/n
2. 皇極：氣初日遲速數 (Δ1+Δ2)/2n + (Δ1-Δ2)/n -(Δ1-Δ2)/2n^2
3. 應天乾元：氣初日盈縮分 Δ1/n + (Δ1-Δ2)/2n
4. 崇玄儀天崇天以後：Δ1/n + (Δ1-Δ2)/2n - (Δ1-Δ2)/2n^2

其中 1、3 等價，2、4 等價，在 1、3 的基礎上考慮半日差卽爲 2、4。經驗算，算法 4 與招差術結果相等。

儀天採用公式進行計算，其公式是完全精確的王榮彬中國古代曆法的中心差算式之造術原理，所以理論上來講可以用儀天公式來代替其他各曆的表格，只需修改系數卽可。儀天象限採用定氣，卽 88.9、93.7 兩種，盈縮積、朏朒積在二分 88.9 日達到極值；而表格法宋曆都用的平氣，在 91.3 日達到極值，我把象限統一爲 91.3 日。以紀元爲例驗算，公式算法與表格算法存在不可忽視的差別，看來並不能用公式代替表格，只能用招差術。這是表格各氣二次差不同造成的，儀天公式默認的前提是一象限中各氣二次差相等。

至於不等間距內插的曆法，經驗算，大衍、宣明公式與拉格朗日內插等價。

再看月離表的算法。皇極一直到崇玄，月亮改正都用等間距二次內插，並且都進行了第二遍修正，交食用二次內插，注曆用線性內插。但是第二遍修正太麻煩了中皇極、大衍相關部分寫了第二遍修正的算法，我暫時忽略，只用招差術進行第一遍二次修正。到了宋曆，月離全都僅僅是線性內插，一下簡單不少，如崇天：

求朔弦望入轉朏朒定數：置所入轉餘，乘其日損益率，樞法而一，所得，以損益其下朏朒積爲定數。其四七日下餘如初數下，以初率乘之，初數而一，以損益朏朒爲定數。

宋曆無一採用二次內插進行月離改正。

經過以上梳理，眉目終於清楚了：

• 【唐曆】交食：二次日躔 + 二次月離。定朔：二次日躔 + 一次月離
• 【宋曆】交食、定朔：二次日躔 + 一次月離
• 【授時】交食、定朔：三次日躔 + 三次月離

欽天步月

授時編製曆書時用立成表來線性內插，立成是用三次內插函數編製的，一近點月分 336 限，所以可以用線性來代替三次內插。授時月離立成大槪受到五代王樸欽天的啓發，欽天月行析爲 248 限，用二次內插編製立成，用立成取代以往的每日月離表，編製曆書時直接用線性內差。

在唐代，只有交食用二次內插，一般注曆用線性內插，到宋代，乾脆交食也只用線性內差了。王樸批評道：

自古朓朒之法，率皆平行之數；入曆旣有前次，而又衰稍不倫。降及諸曆，則疎遠而多失。

「衰稍不倫」大槪指線性內差誤差很大。248 限的好處是省去「皇極舊術，則迂迴而難用」的計算之煩，又能夠非常接近二次內插的效果，達到「衰稍有倫」的理想狀態。欽天的算法爲曆法史上的唯一，「今以月離朓朒，隨曆校定，日躔朓朒，臨用加減。」先計算日躔朓朒，加在經朔入轉上，得「入離定日」，再來計算月離朓朒。這樣從理論上來講比直接用經朔入轉準確，卽「入曆旣有前次」，不明白的是爲什麼後世不延用。欽天近點月分 248 限，程節 800，算來 248 * 800 = 198400 ，和轉分 198393.09 差一些，但這點誤差落在了小數點後 5 位，不會造成任何影響。

可惜欽天躔離表沒有流傳下來，我只好將五紀、紀元月離表平均，用二次招差術歸算爲 248 限立成，進行線性內插。看到疇人傳說歐陽公不懂曆法，看到躔離表太繁雜，索性刪掉，可恨可恨啊！

授時步日躔

太陽在冬至速度最快，夏至速度最慢。冬至到夏至的半歲爲盈曆，夏至到冬至爲縮曆。
秋正__縮末限 88.909225 日__冬至__盈初限 88.909225 日__春正__盈末限 93.712025 日__夏至__縮初限 93.712025 日 秋正

縮末限、盈初限等分爲 6 段，每段約 14.82 日，各段積差爲段末實行度與平行度之差。積差/積日 = 日平差、盈加分，卽平均每日多走的分數。各段日平差與後段日平差相減爲一差，一差與後段一差相減爲二差。

冬至前後：

• 泛立積差 0.69008362180639865
• 平差 (泛平積差 - 泛立積差)/段日 = 2.45538585649203063124214613275506563014130423474055
• 立差 泛立積差/段日^2=0.00314275533037503126

夏至前後：

• 泛立積差 0.6650565922569702
• 平差 (泛平積差 - 泛立積差)/段日 = 2.20748194450453482997512859208836859517228445335591
• 立差 泛立積差/段日^2=0.002726280004867184

冬夏至後 x 日的 日平差、盈縮差 = 定差 x - 平差 x^2 - 立差 x^3 * 10^-4

授時步月離

授時一箇近月點分爲 4 象，每象分爲 7 段，每段分爲 12 限，一轉周 27.5546 日有 336 限。每象 6.88865 日，每段 0.9840928571428571 日，每限 0.0820077380952381 日。
入轉日__疾初限__84 限__疾末限__轉中 168 限 13.7773 日__遲初限__252 限__遲末限__入轉日 27.5546 日

這是授時的月遲疾積度唐宋稱朓朒函數 f(限) = (11.11 限 - 0.0281 限^2 -0.000325 限^3)/100：

月亮改正在四箇象限都是對稱的，授時近點月 27.5546 日分 336 限，每限 0.082，一象限爲 6.888625 日 84 限，取該函數 0–84 的這一段。從圖像可知極值 f(81.748) = 5.429，所以在 81.748–84 之間還有一點小小塌陷。朓朒極值 5.429 度 / 13.36875 度每日 = 0.4061 日

公式源於這箇差分表：

又想到，之所以宋代只有明天用公式計算月離，其他都用表格，因爲遲疾差積在轉折點附近有比較大的停留，而二次函數不能擬合這種停留。直到授時發明三次內插，纔能完美替代表格。太陽盈縮差積的停留不那麼明顯，用二次函數就能比較好地擬合，與三次函數的誤差不會太大，所以宋代儀天、明天、觀天都用公式代替表格。紀元爲了追求精確，又回到表格的老路上。

時憲曆日躔

《新法曆書》用對分圓模型，《曆象考成》用本輪均輪模型。下圖是兩條曲線，可見幾乎重合，只有在極值附近才分開了一點。《新法》極值是$(88.973,2.05335)$，《考成》是$(88.973,2.05302)$

時憲曆月離

《新法》和《考成》月離初均如下圖，極值爲$(91.662,-4.974295)$。時憲曆日躔從近地點起算，月離從遠地點起算。

日軌

黃赤轉換

古代天文模型是以赤道爲基準，所謂「赤道者，常道也，其數常定，紘帶天中，儀極攸準」，黃道度要根據赤道轉換而來。

度數從冬至起算，二至到二分：赤大於黃；二分到二至：黃大於赤。只有紀元有黃轉赤公式，其餘只能赤轉黃，我用與紀元相同的求反函數思路，推導出各宋系曆法的黃轉赤公式。小數點後 4 位的精度是 0.36”

纪元历利用求根公式给出了二次函数的反函数，将唐代边岗的双二次函数改造成了一套漂亮的二次复合函数，这个大体上等价于对三角函数用泰勒级数展开以后的前 4 次项结果。在误差上，当角度大于 40 度时，他的算法的精度比泰勒级数还要好。

黃赤轉換公式的推導：

• 大衍等曆的黃赤轉換表格是用等差級數構造的。設歸算到半象限之內的赤道度爲 $x$，黃道度爲 $x_1$，「初率」爲 $e$，「每限增減」爲 $-f$，分母爲 $g$，每「限」長度爲 $s$
• 代入等差級數公式 $S_n=n[a_1+\frac{(n-1)d}{2}]$，其中 $n=\frac{x}{s},a_1=\frac{e}{g},d=-\frac{f}{g}$，可得 $S_n=\frac{x[s(2e+f)-fx]}{2gs^2}$
• 令 $a=s(2e+f),b=2gs^2,c=f$，得 $\Delta_{eq\rightarrow ec}=\frac{x(a-cx)}{b}$，即紀元等曆的赤轉黃公式
• 求 $x-\Delta_{eq\rightarrow ec}$ 的反函數，得 $h=\sqrt{(\frac{b-a}{2c})^2+\frac{b}{c}x_1} - \frac{b-a}{2c}$，即紀元曆的黃轉赤公式
• 黃轉赤之差 $\Delta_{ec\rightarrow eq}=abs(x_1-h)$，最後根據象限取適當的符號。
• 皇極、大衍、乾元、儀天有「依平」，到 45 度即止，45–半象限之間爲 45 度的值，所以要設取值範圍。皇極是 $f(x){max}=f(44)$，其他幾部 $f(x){max}=f(45)$。欽天、應天略有不同，函數的極值不到 45， $f(x)_{max}=f(\frac{a}{2c})$

更多見《中國古曆通解》討論大衍曆 p215、欽天曆 p496、應天曆 p523。崇玄曆的黃赤轉換公式比較特殊，不在討論範圍之內。

積度轉宿度

下表據授時曆議及各曆。空白爲同前。

先秦時期的赤道宿度已不可俱考，但是出土材料能提供很多線索。到太初改曆，赤道宿度就固定下來了，太初的赤度一直沿用到唐初。大衍重新制定了一份赤度表，沿用到宋代。明天重新定出一份赤道宿度表：

自漢太初後至唐開元治曆之初，凡八百年間，悉無更易。今雖測驗與舊不同，亦歲月未久。新曆兩備其數，如淳風從舊之意。

以從舊之誼，明天還是沿用大衍的赤度表。直到北宋最後一部曆法紀元又做出調整。紀元觀測精度達到 0.25 度，授時達到 0.05 度。如果單從數字改變幅度來看的話，影響最深的是太初和紀元的赤度表。

而黃道觀測結果就更迭得頻繁得多，想看具體情況，可以看我的源代碼。

這箇工具提供了各曆的宿度轉換，需要根據年代選用當時的曆法：太初前 104 – 麟德665– 大衍729 –應天964–明天1065–紀元1106 或重修大明1180–授時1281

斗分

「斗分」是什麼意思呢？歲實回歸年長度= 365 + 斗分 / 度法當然，不同曆法有不同的名字。黃初作者韓詡認爲乾象「減斗分太過，後當先天」，大槪就是比較早的出現「斗分」一詞的材料了。爲何要叫「斗分」？中國古代一週的度數是歲實，所以每部曆法都有各自的圓周度數，而我們看太初的赤度表，發現其中都是整數，沒有小數，這是怎麼回事？一般而言，小數點要加到斗宿的後面，所以叫 斗分 ，曆法術語是「經斗去分」。到了祖沖之將歲差引入曆法後，各曆上元日所在赤度一般在虛，所以小數點加在虛宿後面，卽「經虛去分」。因此唐代以後，「斗分」一詞就不再用了，否則就要叫「虛分」了。

黃道過宮

以後補充。直到時憲曆，宮纔固定是十二中氣，此前都沒有對應起來。

里差

庚午是唯一有里差地理東西時差的古曆：

求朔弦望中日以尋斯干城爲準，置相去地里，以四千三百五十九乘之，退位，萬約爲分，曰里差。以加減經朔弦望小餘，滿與不足，進退大餘，即中朔弦望日及餘。〔以東加之，以西減之。〕

算了重修大明和庚午，庚午經朔正好少了 1700 分，24 * 0.17 = 4.08 時 = 2.04 辰，結合 郭津嵩：撒马尔干的中国历法——蒙古扩张中的知识变动及其文化因素，「撒马尔干与燕京之间距离和时差的估计分别是二万里和二时」，考慮到修正因素，則尋斯干城與中國都城正好相差 2 辰。另外，里差並無球面三角經度的意義，只表示地表距離。

里差 = 里 * 4359 / 10 /10000，尋斯干城與中國都城的里差是 20000 * 0.04359 / 日法 5230 = 0.16667 日，正好 2 辰。庚午經朔比重修大明減少 33.3333 / 5230 = 0.63735 刻。撒馬爾罕在 67°E，北京在 116°E，時差 3.27 小時，遠小於 4 小時，耶律楚材高估了兩地距離。

里差怎麼用？

求天正冬至置上元庚午以來積年，以歲實乘之，爲通積分；滿旬周，去之；不盡，以日法約之，爲日，不盈爲餘⋯⋯〔先以里差加減通積分，然後求之。〕

求冬至赤道日度置通積分，以周天分去之⋯⋯〔其在尋斯干之東西者，先以里差加減通積分。〕

求經朔弦望入轉置天正朔積分，以轉終分及秒去之，不盡，如日法而一，爲日，不滿爲餘秒，即天正十一月經朔入轉日及餘秒⋯⋯〔加減里差，即得中朔弦望入轉及餘秒〕

求朔望入交〔先置里差，半之，如九而一，所得依其加減天正朔積分，然後求之。〕置天正朔積分，以交終分去之

求五星天正冬至後平合及諸段中積中星置通積分，〔先以里差加減之。〕各以其星周率去之，不盡，爲前合分

先把里差加在通積分上，接著按一般步驟求冬至、冬至日度、五星前合分。求經朔入轉，先用朔積分求得入轉日，再加減里差。「朔積分」是用沒有加減里差的通積分求得的：「置通積分，滿朔實去之，不盡，爲閏餘；以減通積分，爲朔積分」。稍微麻煩一點的是入交，里差 / 2 / 9 加到朔積分上，再求入交，爲什麼要除 18 呢？按這樣的方法加上里差後，庚午比大明入轉日多 0.02 日，入交日少 0.002 日，幾乎沒區別。

步晷漏

假設 1 尺 = 20 cm，小數點後 4 位是精度就是 20μm。日出時刻 = 夜半漏 + 一般 2.5 刻一日百刻。由時憲曆書可知，清代是把日出到日入算晝刻，日入到日出算夜刻，不包含晨昏蒙影。

赤緯

陳美東中國古代太陽視赤緯計算方法：各曆法赤緯誤差度：四分 0.7，麟德 0.13，大衍 0.06，宣明、儀天 0.45，崇玄 0.09，崇天 0.23、明天 0.2，觀天 0.21，紀元、授時 0.11。各曆漏刻誤差分鐘：授時 0.7、乾元、紀元、重修大明、庚午 3.8，四分、景初、元嘉 4.4，崇玄 4.6，大明 4.7，皇極 5.6，大業戊寅 6.1，麟德 4.6，明天、觀天 4.9，大衍 5.1，崇天 6.2，宣明 7.7，儀天 7.9。

漏刻觀測地點

各曆晷影觀測地點及緯度北極出地，現代度數用「°」，古度用「度」。詳見陳遵媯《中國天文學史》第八編第一章。

現代測定：[北緯, 東經, 海拔]

• 南京 [32.061, 118.791, 100]（雞鳴山北極閣。明时“国朝于山巅置仪表，以测玄纬，名观象台，更名钦天山”。南朝时为皇家苑囿。明洪武十八年复建观象台。清康熙七年，清皇室将观象台天文仪器全部运至北京）
• 長安 [34.282, 108.964, 405]（假設在大明宮南門）
• 陽城縣 [34.404, 113.141, 265]（登封告成鎭周公測景臺。周公表高1.64m、開元八尺）34.475 度大衍宣明曆測
• 洛陽 [34.696,112.626, 154]（灵台遗址在今偃师县佃庄公社朱圪垱大队岗上村与大郊寨之间。臺高六丈14m）
• 浚儀縣岳臺 [34.813, 114.295, 75]（开封市示范区西郊乡演武庄）34.8 度麟德曆測「唐貞觀初，李淳風於浚儀縣古岳臺測北極出地高三十四度八分」
• 大都 [39.906, 116.428, 60]（建國門觀象臺）40.95 度授時曆四十度太強 39.9917°（清代）

據陈美东《中国古代昼夜漏刻长度的计算法》：

• 【洛陽】四分、景初、元嘉、大明
• 【長安】皇極、大業、戊寅、麟德
• 【陽城】大衍、宣明、崇玄、應天、儀天、崇天
• 【浚儀】乾元、明天、觀天、紀元、重修大明、庚午

《新五代史·司天考一》（中華，2016，頁756）：

古者，植圭於陽城，以其近洛也，蓋尚慊其中，乃在洛之東偏。開元十二年，遣使天下候影，南距林邑，北距横野，中得浚儀之岳臺，應南北弦，居地之中。大周建國，定都於汴。樹圭置箭，測岳臺晷漏，以爲中数。晷漏正，則日之所至，氣之所應，得之矣。

均方誤差：

太陽赤緯

這是儀天公式（紅、紫）與現代公式（黑）的對比，區別很大，因爲儀天是以距冬至時長爲自變量，他曆和現代公式都是以黃道實行度爲自變量。

晷影

這是《崇玄》晷長公式（紅、紫）與現代算法（黑）的對比，兩者難以區分，非常貼合。

月行九道

黃赤白道示意圖數頁 347：

大衍開始有月行九道法，以步黃道月道之差四季爲節氣，而非月份：

再加上與黃道交會，一共就是九道。崇天曆：

推月行九道：凡合朔所交，冬在陰曆，夏在陽曆，月行靑道；冬、夏至後，靑道半交在春分之宿，當黃道東；立冬、立夏後，靑道半交在立春之宿，當黃道東南：至所衝之宿亦如之。冬在陽曆，夏在陰曆，月行白道；冬、夏至後，白道半交在秋分之宿，當黃道西；立冬、立夏後，白道半交在立秋之宿，當黃道西北：至所衝之宿亦如之。春在陽曆，秋在陰曆，月行朱道；春、秋分後，朱道半交在夏至之宿，當黃道南；立春、立秋後，朱道半交在立夏之宿，當黃道西南：至所衝之宿亦如之。春在陰曆，秋在陽曆，月行黑道。春、秋分後，黑道半交在冬至之宿，當黃道北；立春、立秋後，黑道半交在立冬之宿，當黃道東北：至所衝之宿亦如之。

九道術前身是劉洪乾象月行三道術，只有陰陽黃三道。漢代也有九道術，但是跟唐宋九道術沒什麼關係，漢代九道用來推算月行遲疾。數頁 336陳久金的示意圖：

數頁 341：

交食

我把交會推步分一下階段：

0. 漢代：只能根據食季判斷是否可能出現日月食。
1. 魏晉南北朝：可以計算食分多少，判斷交食程度、虧食所起。
2. 隋唐初大業、戊寅、皇極、麟德：出現時差、食差改正，但相當不成熟，瑣碎不堪複雜無比。
3. 盛唐中唐大衍、五紀、正元、欽天：規範化。宣明之後， 崇玄另起爐灶，五代欽天又回到大衍的思路，把食差加在食限上，而非去交分上。經過一番角逐，最終宣明方案勝出。此前人所未發。
4. 唐後期至北宋前期，宣明：日食三差公式算法確立下來，奠定後世步交會基本模式。此後應天、乾元、儀天都在不斷調整，變動幅度也不小。
5. 崇天以後：成熟定型，此後各曆只有比較小的區別。紀元標誌著完全成熟。這一階段比以往都要簡明精練。

古代判斷交食都是用黃白經差，而月黃緯沒有參與計算，可能只是用來輔助判斷。

參數、槪念

交點月

交點月與食季（單位：朔望月）轉換公式：Node = Lunar * 食季的朔望月數/ (0.5 + 食季的朔望月數) = Lunar * 交點年的朔望月數 / (1 + 交點年的朔望月數)我的獨創發明。皇極是唯一不確定旣有食季又有交點月的曆法，以皇極驗之，分毫不差。大明以前無交點月，只有食季，我藉此全部統一爲用交點月進行計算，非常方便。

（沒什麼用：也就是說 (交點年的朔望月數 +1)/交點年的朔望月數=朔望月/交點月——為什麼呢？？？）

不過乾象有三種交點月，反映出劉洪對交點月的認識還不成熟。

交點退行速度

交點退行速度用此公式計算： Sidereal = (V 平 + V 退) * Node（陳美東《劉洪的生平、天文學成就和思想》，1986），再把月平行速 V 平 = Sidereal/Lunar + 1 公式代入，得 V 退 = Sidereal/Node - Sidereal/Lunar - 1，我們可以用這箇公式計算任意曆法的交點退行速度。明天步交會中的「朔差」表示一箇朔望月交點退行距離藤豔輝宋代朔閏頁 95。

交率交數

關於交率交數，主要參考劉金沂隋唐曆法中入交定日術的幾何解釋，自然科學史研究1983(4)。

定朔入交定日 = 經朔入交泛日 + 日改正 ± 交率/交數 * 月改正

交率/交數 = 交點月/交點年 = (V 日+V 退) / (V 平+V 退) = 27.2122/346.608 ≒ 0.0785 。交率交數是經朔到定朔才用的，計算其他時候的不用管，某時直接加減月亮改正即可。

經過驗證，這箇公式完全可靠。計算以下幾部曆法：

• 紀元交率/交數 324 / 4127 = 0.07850739，精確値爲 7323715785246679/93286970952593250 = 0.078507381 精確到了小數點後 7 位，非常棒。通過「同餘」標籤下的連分數計算，可見紀元交率是精確值的一箇漸進分數。
• 觀天 183 / 2331 = 0.07850708，精確值爲
  3271955768163223/41677024412605020 = 0.078507422597416
  精確到了小數點後 6 位。
• 重修大明10/127 = 0.07874，精確值
  4098461650124679/52204833831588280 = 0.0785073
  有些出入。
• 欽天 72 / 963 = 0.0747664，精確值 5214687527858525/66791617777516270 = 0.078074
  相差有點遠。刘金沂最後提到藪內清有一種近似算法，交率/交數=0.0748，這正是欽天曆的值。

食限

宣明、應天、乾元、儀天陽曆食限 4.2 度左右，陰曆 9.6 度，崇天、觀天陽 5.3，陰 8.84，紀元陽 4.88，陰 9.76，授時陽 6，陰 8。

時差

古曆日食時差是基於定朔時刻 r 的一元函數，R = | 0.5 - r |，則 時差 = kR(0.5 - R)。但理論上還應該考慮太陽黃經，如果授時曆加上一箇黃經的線性函數，就能很好地與理論曲線脗合。

食差

食差是對日食視差影響的修正。由於視差，視月亮位置總是比眞實位置低，古人用相對的模型，視太陽、視黃道比眞實位置高，可以用此圖幫助理解這箇思路是我自己想的：

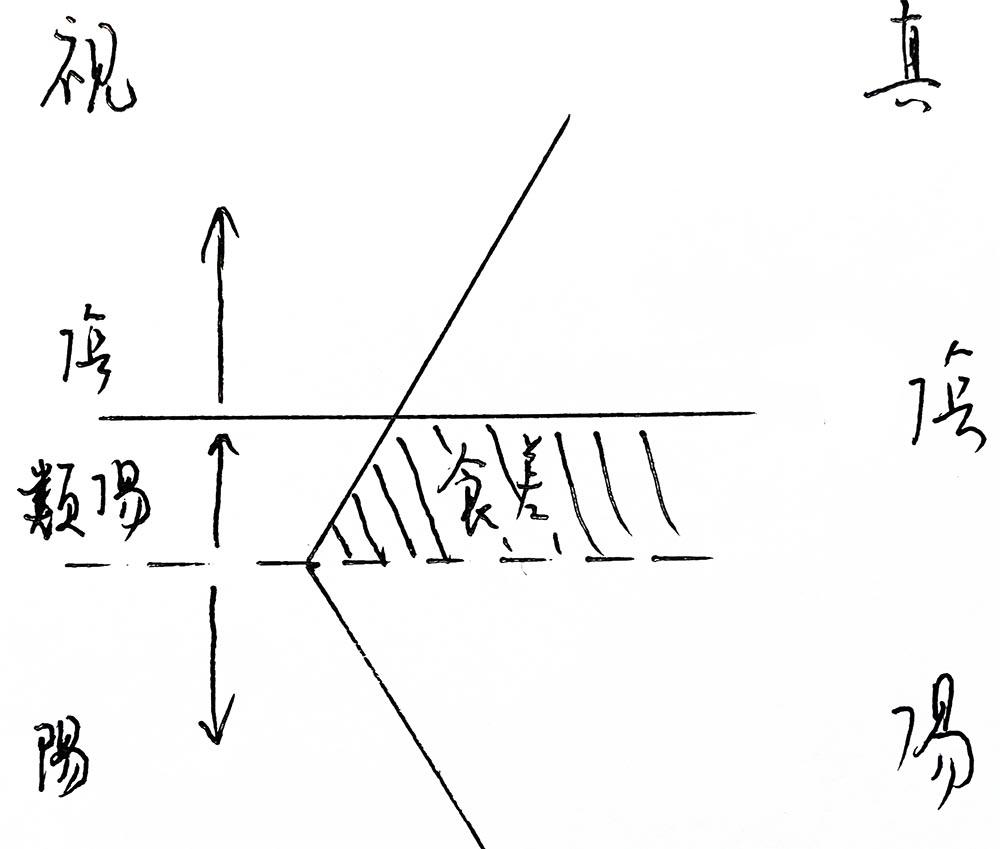
虛線是眞實的黃道、陰陽曆分界線簡稱眞陰陽界，以上是陰曆，以下是陽曆，實線是視黃道、視陰陽界，虛線到實線的距離就是食差，豎著的兩條折線是食限月道當然是一條直線，我只是爲了好看，月亮在食限之內則食。實線以上的區間 A 是陰曆，實線到虛線之間的區間 B 是類同陽曆，虛線以下的區間 C 是陽曆。由於視陰陽界移動到了實線，區間 B 的眞位置雖然是在陰曆，但視位置是在陽曆，所以叫類同陽曆。去交分從眞陰陽界起算，箭頭方向表示增減方向；食分則以視陰陽界爲標準，離視陰陽界越近，食分越大；所以在陰曆和陽曆，都是去交分越大，食分越小，而在類陽曆，去交分越大，越靠近視陰陽界，食分越大。大衍、欽天是把食差加在陰陽界上，去交分不動，而宣明及後世曆法是把食差加在去交分上，陰陽界不動，兩者都是一箇意思。有了這樣的認識，我們就能很快理解各曆術文。

書上看到的：食差只與月亮天頂距有關，與午正前後無關，古曆卻將此作爲正負判斷依據，完全不對，只能是正誤參半。

階段四五步交會

本文是一箇提綱，主要目的是明晰各曆槪念的區別、各算法的自變量，這是最要命的。相關論文也有，但是看得不明不白，只好自己根據宋志等原文重新理一遍。

爲節省篇幅，「入交」表示加時入交日及餘分或餘秒。日月改正包含以距離爲單位的先後積和以時間爲單位的朏朒積，我統一稱爲日月改正，讀者需加以區分凡言積度，則爲先後積；凡言入交，則爲朏朒積。需要注意各名詞的細微區別，可能一字之差就完全不同。月改正 (定朔入轉) 表示以定朔入轉爲自變量的月改正，午前後分 (定餘) 表示午前後分以定餘爲自變量。「朔」指「朔望」。比例指 交率/交數 ≒ 0.0785，各曆比例不同。日月改正爲太陽改正、月亮改正相加減。

南宋各曆全同紀元；遼金系和紀元很像，除了單獨說明的，其他基本上都是紀元。

〇、布算

大業：「日出前入後各二時外，不注日食。」戊寅：日出後日入前一時半12.5 刻，不注月食，麟德再加上：晨昏之間不可見食甚。大統：「定朔小餘在日出前日入後二十分已上者，日食在夜；定望小餘在日入前日出後八刻二十分已上者，月食在晝——皆不必布算。」不知道「日入後二十分」中間是不是漏了幾刻。授時日食時差的極大值是 6.5 刻，半食延的極大值是 5.74 刻，那麼日入後應該就看不到初虧了，所以就是二十分，沒有漏。其他曆法就不知道什麼情況了。

入交

「定朔入轉」的槪念也困擾我很久，終於在授時找到解釋：

置經朔弦望入轉日及分，以定朔弦望加減差加減之，爲定朔弦望加時入轉；以定朔弦望日下分減之，爲夜半入轉。

大統：

置經朔弦望遲疾曆，以定朔弦望加減差加減之。在疾曆，便爲定朔弦望加時入轉日；在遲曆，用加轉中。置定朔弦望加時入轉日，以定朔弦望小餘減之，爲夜半入轉日。

所以定朔入轉 = 經朔入轉 ± 日月改正。

天正經朔入交應天：中盈度，乾元：平交朔日

經朔夜半入交 = 經朔入交 - 小餘。

定朔夜半入交：整數日有進退的，加減一日，否則因經爲定只有夜半是這樣，如果加時，就要相應加減了。

明天求去交度分的算法很獨特，交初度 = Sidereal - 積月 * 朔差 % Sidereal，翻譯過來，就是上元以來交點退行的距離，再反減。這樣得到的是正交距冬至度數，另外再根據太陽距冬至度數，得出交前後分。

入陰陽曆

朔入交常日 = 經朔入交 ± 日改正應天：朔交初度分，乾元：朔交分

【欽天乾元儀天崇天觀天遼金】朔入交定日 = 朔入交常日 ± 比例 × 月改正乾元：度定分

入陰陽曆 ()：

• 【應天】朔入交常日 ± 月改正卽紀元的定朔入交泛日。很奇怪，不確定是不是這樣
• 【應天乾元儀天崇天觀天遼金】朔入交定日

交前後分 (入陰陽曆)

不論陰陽，近交初爲交初，在二十六日、二十七日爲交初；近交中爲交中，在十三日、十四日爲交中。交初交中主要用來判斷食差符號。

【紀元】食甚泛餘 = 經朔 ± 日月改正 (朔入氣入轉) ± 日月改正 (朔入氣入轉) * 損益率 (定朔入轉) 「朔入氣入轉」我暫時處理爲平朔

【遼金】遼金系和紀元很像，除了直接以入交定日入陰陽曆，以及這條：食甚泛餘 = 經朔 ± 日月改正 (朔入氣入轉) * 1337 / 轉定分 (定朔入轉) 。

• 關於「泛餘」，紀元：

  以其朔望入氣入轉朏朒定數，同名相從，異名相消，副置之；以定朔、望加時入轉算外損益率乘之，如日法而一⋯⋯所得，視入轉，應朒者依其損益，應朏者益減損加其副；以朏減朒加經朔望小餘，爲泛餘。

  上文說過，唐宋以來躔離分母都是月平行速，這樣並不精確，這裏的泛餘實質上就是以月實行速爲分母的躔離。如果紀元還不好理解，那重修大明就非常明白了，乘月平行速，除月實行速，就等於把分母替換成了月實行速。紀元與重修大明幾乎等價。

【崇玄】定朔入交定積度 = 入交常日 * 月平行速沒說入交常日是什麼，但是檢索交率、交數，發現只在列參數的時候出現一次，那麼很可能「入交常日」就是宋曆的「入交定日」。

【崇天觀天】月入陰陽曆積度 = 入陰陽曆 * 月平行速

【紀元庚午授時】定朔入交泛日 = 經朔入交 ± 日月改正

【紀元庚午】定朔入交積度 = 定朔入交泛日 * 月平行速

【授時】交常度 = 經朔入交 * 月平行速

【紀元庚午】定朔入交定積度 = 定朔入交積度 ± 月改正 (定朔入轉)

【授時】交定度 = 交常度 ± 月改正 (經朔入轉)

時差

只有紀元、授時有月食時差，其他都以定望爲食甚。

【應天乾元儀天崇天】午前後分 (定朔) 宣明：初率末率，欽天：距午分，授時：中前後分

【紀元庚午】中前後分 (泛餘)

【宣明應天乾元儀天】時差 (午前後分，半晝分)

【欽天崇天觀天授時】時差 (午前後分)

【紀元】時差 (中前後分)

【欽天應天乾元儀天崇天】食甚定餘 = 定朔 ± 時差

【明天】食甚 = (經朔 ± 月改正) * 月平行速/月實行速 ± 日改正

【紀元】食甚定餘 = 泛餘 ± 時差。

【應天乾元儀天崇天授時】距午分 = 午前後分 + 時差應天：距中分，乾元：距午刻分，崇天：午前後定分、距午定分。注意，這裏是都加不減，紀元分加減：應天「以差皆加午前後分，爲距中分」乾元「皆加午前、後分，爲距日分；刻法而一，爲距午刻分」崇天「以時差加午前後分，爲午前後定分」，授時「以中前後分各加時差，爲距午定分」。宣明是食甚時刻，之前皇極等等大槪是定朔

儀天有一句很難懂：「置月行去交黃赤道差，視月道差，如黃赤道交者，依其加減；不如黃赤道交者，返其加減；定朔、望小餘爲食甚餘，亦返其加減去交定分。」存之再慮。

【明天觀天紀元】午前後分 (明天觀天：食甚，紀元：定餘)

氣差

氣差欽天：黃道出入食差，應天、儀天：黃道差，乾元：晷差，明天、授時：南北差

【應天乾元儀天崇天】氣差 (定朔距冬至日，距午分) 應天：朔定積，崇天：朔中積，那就當成定朔，觀天：盈縮限度及分

【宣明觀天】氣差 (定朔距冬至日，午前後分) 宣明沒說是定朔還是經朔距冬至，但差別應該不大

【明天紀元授時】食甚距冬至日 = 經朔距冬至日 + 食甚 - 經朔明天：朔加時中日 = 朔中日 + 加時小餘 - 經朔小餘，紀元：食甚入氣 = 經朔入氣 + 食甚 - 經朔

【明天紀元授時】食甚日行積度 = 食甚距冬至日 ± 日改正 (食甚) 明天：朔加時定日

【明天紀元】氣差 (食甚日行積度，午前後分)

【授時】氣差 (食甚日行積度，距午分)

冬至前後符號：

宣明氣差「秋分後，陰曆減之，陽曆加之。」應天赤道差「盈初縮末內減外加」，乾元離差「秋分後陰減陽加」，紀元氣差「夏至後末限、冬至後初限，〔交初以加，交中以減。〕」崇天「秋分後，交初以加，交中以減」，庚午「秋分後陽曆加陰曆減」。

授時「在縮初盈末者，交前陰曆加陽曆減，交後陰曆減陽曆加」相當於交初交中。大統「縮初盈末，食在正交爲加，中交爲減」

刻差

刻差欽天：黃道斜正食差，應天、儀天：赤道差，乾元：離差，明天、授時：東西差

【應天乾元儀天崇天】刻差 (定朔距冬至日，距午分)

【觀天】刻差 (定朔距冬至日，午前後分)

【明天紀元】刻差 (食甚日行積度，午前後分)

【授時】氣差 (食甚日行積度，距午分)

盈曆冬至後符號：

宣明刻差「冬至後食甚在午正前，夏至後食甚在午正後，陰曆以減，陽曆以加。」應天黃道差「入盈，以定分午前內減外加」，儀天黃道差「冬至後，甚在午正東，陰減陽加；甚在午正西，陰加陽減；夏至後卽返此。」紀元刻差符號「冬至後食甚在午前，夏至後食甚在午後：交初以加，交中以減」，崇天「冬至後食甚在午前，夏至後食甚在午後：交初以加，交中以減」，庚午「冬至後午前陽加陰減」。

授時東西差「在盈，中前者，交前陰曆減陽曆加，交後陰曆加陽曆減；中後者，交前陰曆加陽曆減，交後陰曆減陽曆加。」

加差

只有宣明、儀天有加差。

符號：宣明「若蝕甚在午正後，則每刻累益其差，陰曆以減，陽曆以加。」

【宣明應天乾元儀天明天紀元授時】食差 = 氣差 ± 刻差 ± 加差明天：食差總數 【崇天觀天】食差 = 氣差 ± 刻差 ± 時差

食分

除了【紀元授時】距交分 = 交前後分 ± 食差乾元：定交分，宣明儀天明天：去交定分，崇天觀天：交前後分，判斷是否返入內外道，陰曆食陽曆不食。

【紀元】朔入交定日 = 入交常日 ± 食差 ± k0。望入交定日 = 入交常日 ± 比例*月改正 (望入轉)卽乾元儀天的入交定日

【紀元】入陰陽曆 (入交定日) 。交前後分 (入陰陽曆)

【授時】正交中交限 = 正交中交度 ± 食差。正交度 357.64 = 交終度 - k06.1534，中交度：188.05 = 交終度/2 + k06.1533。交前後度 (正交中交限，交定度)。不同的是，食差並不是加在交定度上，而是正交中交度，這樣的話符號就跟唐宋曆完全相反了，復檢術文，符號確與唐宋曆相反。爲統一起見，我把食差、k0 加在入交度上，符號就與授時術文相反。曲安京數理頁 451：根據黃白交點距離常數交終度交中度換算出黃道與視白道的距離正交中交限。

【應天乾元儀天】日食分 (距交分，定餘)

【應天乾元儀天】月食分 (距交分)

【欽天崇天明天觀天紀元授時】食分 (交前後分，明天：去交定分)

月食旣內外分

食延

【應天】定用分 (食分，月實行速)

【乾元】定用分 (食分)

【儀天】定用刻 (食分，去交定分)

【崇天明天觀天授時】日食定用分 (食分，月實行速)

【崇天明天觀天】月食定用分 (交前後分，明天：去交定分，月實行速)

【紀元】定用分 (交前後分，食甚入轉損益率)

紀元月食半食延的最大值是 656 / 日法 7290 * (1 + 726 / 7290) = 9.895 刻。

這是授時月食定用分函數爲便觀看，放大 10 倍：

f(食分) = sqrt((30 - x)x) * 0.00574 / 1.0962，極值 f(15) = 0.0785 日。1.0962 是月亮每限平行度，化爲每日平行度就是我們熟悉的 13.36875，0.574/1.0962 = 7/13.36875

以下是各曆定用分的分配，數字的單位是定用刻、定用分。

計算食延一般來說只涉及食分，但也有幾部曆法用到了去交定分：儀天、明天、崇天觀天、紀元。

另外，授時曆經、大統曆志定用分的分母「如定限行度而一」，正常理解的話就是月實速，但大統通軌、大統曆志在羅列日食用數時這樣解釋「定限行度」：「視同定限下遲疾行度⋯⋯全分內減去日行分八分二十秒，餘爲定限行度也。」「以定限，取立成內行度⋯⋯內減日行分八分二十秒」也就是說還要減去日平行速。而躔離改正不用減日平行，大統曆志步月離的分母：「以所入遲疾限下行度而一」。授時曆經沒有說，但可能是和大統一樣的處理方式。我聽說有種很普遍的說法是大統的躔離改正分母要減去日平行速，這是比授時進步的地方，這應該是一種誤解，卽使要減，也是在求定用分的時候，而不是躔離改正的時候。

虧蝕所起方位

無關緊要，略

帶食出沒

宣明以後有了帶食計算：

凡日月帶蝕出沒，各以定法通蝕分，半定用刻約之，以乘見刻。多於半定用刻，出爲進，沒爲退。少於半定用刻，出爲退，沒爲進。各如定法而一，爲見蝕之大分。

說了半天，帶食分其實就是可見食延和眞實食延的線性關係，非常簡單。崇玄也是線性關係。欽天在此基礎上加入了距食分的因素，有了些進步。

⋯⋯

階段三步交會

大衍

入交定日。初步判斷入食限

月食

去交前後分 (入交定日)

食分 (去交定分)

日食

入氣差積 (距冬至日)

朔定差及定限 (入氣差積)

入陰陽曆

⋯⋯

時差

五紀

五紀、正元是唯一有月食食差的曆法。

五紀跟宣明很像了，是把食差加在去交分上，但是還有交前交後之別，尚不成熟。

一項加在陰曆、類陽曆上的食差：

自大寒畢立春，交前五辰外，自大暑畢立冬，交後五辰外，又減一辰。

基於夏至前後對稱，以及覆蓋範圍連續性，我覺得應該改爲「自大寒畢立夏」。但後來發現，五紀原來是照抄麟德：

大寒畢立春，交前五時外、大暑畢立冬，交後五時外，皆減一時；五時內者，加一時。

非常難辦，不大可能兩部曆法都產生相同的訛誤吧？那只能這樣理解：「大寒畢立春」是立春前後一氣，「大暑畢立冬」是秋分前後四氣。

崇玄

崇玄的食差算法非常獨特，曲安京直接一筆帶過，說天文含義不明。我來梳理一下。

1、置其朔距天正中氣積度，
2、以減三百六十五度半，餘以千乘，滿三百六十五度半除爲分，曰限心。加二百五十分，爲限首。減二百五十分，爲限尾。滿若不足，加減一千。 3、退蝕定餘一等， 4、與限首尾相近者，相減，餘爲限內外分。 5、其蝕定餘多於限首、少於限尾者，爲外；少於限首、多於限尾者，爲內。

1、「距天正中氣積度」找不到解釋，上文步晷漏的自變量是「二至加時已來至其日昏後夜半日數及餘」，那積度應該指加上了日躔的實行度。

2、「滿若不足，加減一千」，就要用到 mod：

1
2
3

C = (365.5 - 積度) / 0.3655 // 限心。舉例: C(182.5)≒49.317872
L = (C - 250 + 1000) % 1000 // 限尾。L(182.5)=799.317872
R = (C + 250 + 1000) % 1000 // 限首。R(182.5)=299.317872

3、「蝕定餘」是食甚時刻的約餘萬分小數，比如一日的 0.75 就是 7500，再退一等得 750。

4、限內外分的算法：min(abs(食甚 - R), abs(食甚 - L))，這樣就能求得與限首尾相近的了。

5、蝕定餘和限首尾比較，得出限內外。可見限內外是與距冬至積度、食甚時刻有關的二元一次函數。

藍色限首 R，綠色限尾 L：

另外一箇關鍵點是，「多於限首、少於限尾者」不應該是同時滿足，而是滿足其中之一卽可，否則很多區間旣不在限內，也不在限外。據此可以作下圖：

與其他曆法的氣差刻差符號不同，崇玄的限內外標準是流動的，沒有固定的午前午後或者冬至後夏至後。

欽天

欽天日食分：

以定準加中限，爲陰道定準；減中限，爲陽道定限。不足減者，反減之，爲限外分。視陰道距交分，定準以上，定限以下，爲陰道食；卽置定限，以距交分減之，爲距食分。定準以下，雖曰陰道，亦爲陽道食；卽加陽道定限，爲距食分。其有限外分者，卽減去限外分，爲距食分。不足減者，不食。其陽道距交分，定限以下，爲入定食限；卽用減陽道定限，爲距食分。

很迷惑。我索性這樣改：

以定準加中限，爲陰道定限；減中限，爲陽道定準。不足減者，反減之，爲限外分。視陰道距交分，定準以上，定限以下，爲陰道食——卽置定限，以距交分減之，爲距食分。定準以下，雖曰陰道，亦爲陽道食——卽加陽道定準，爲距食分。其有限外分者，卽減去限外分，爲距食分；不足減者，不食。其陽道距交分，定準以下，爲入定食限；卽用減陽道定準，爲距食分。

這樣就非常通暢了。

階段二推遊交

大業戊寅

這兩部曆法推算交食都考慮了五星的因素，這是很神奇的思路，當時人爲什麼覺得五星對交食有影響呢？值得探討一下。也許因爲星和日月有牽制作用？